My ultimate automotive engineering nerd out essay
#1
This essay is the result of a note on facebook that I've worked on over sophomore all the way into senior year of Mechanical Engineering school at Colorado State University. It's very informal in set up, not at all professional. But I have a burning desire to share what I've learned. Honestly, alot of this stuff I wrote from sophomore year I don't really even remember. Triple integration is something I haven't done in ages. Its all been single and double integrals.
I'm not at the knowledge level of Engineering Explained's Jason Fenske, but he has helped me learn.
Here it is, almost nobody on facebook reads it LOL
Please, if anything is wrong, and some things are a bit assumed, let me know. I want to learn.
Rocket engine nozzles typically feature a shape that first converges then diverges. This is because the flow of the air fuel combustion reaction enters the nozzle at a subsonic velocity, below the speed of sound. As the nozzle converges, the flow's velocity increases to a sonic velocity that forms a shockwave infront of it as pressure decreases. It has reached a speed of sound with a Mach number of 1. Then the nozzle begins diverging, because the flow is supersonic. The conditions for supersonic flow are inverted, so the nozzle diverges to increase velocity. Pressure continues to decrease. In the design of the NASA space shuttle, the cooling system of the divergent supersonic flow rocket engines borrowed cooling techniques used in 1880s internal combustion engines.
Cars- what amazing marvels of technology. Perhaps one of the most taken for-granted products in people's lives. Cars are likley the most technologically complex possession in the average person's life. Modern cars are the result of exhaustive computational analysis in fluid mechanics to design an aerodynamic body, involving super computers calculating multivariable calculus and partial differential equations at incredible speed. The 1989 Lexus LS400 was the result of some 1400 engineers working tirelessly. Internal Combustion Engines are absurdly complex, involving fluid mechanics, thermodynamics, chemistry, and engine dynamics. Transmissions are even more mind boggling, containing approximatley 700 parts.
In designing automotive camshafts, when choosing calculus/differential equation based piecewise functions for your displacement model, one must choose a function which will not "run out" of derivatives from displacement in which ds/dt is velocity, in which dv/dt is acceleration, and da/dt becomes jerk. It is then often necessary to select a sinusoidal or cosine type function which derives and integrates between cosine and sine, and therefore does not encounter a "Dirac delta function", which results in infinity spikes starting at acceleration and passing on to jerk, which theoretically states that the cam lobe is experiencing zero stress and force. This is the opposite of the truth, as this would result in a sharply pointed cam lobe, which would experience massive stress concentration at its tip, which would rub off into a blunter normal shaped cam from the incredible stress. In calculus, these "Infinity spikes" are the results of vertical lines in the velocity diagram which creates discontinuities. A dwell is a location where a cam lobe has zero velocity and acceleration. Non-dwell piecewise functions at non-zero velocity and acceleration must be linked continuously to dwells with zero velocity and acceleration according to the fundamentals of cam design.
A multivariable Riemann sum in calculus can be used to approximate any 3 dimensional volume by approximating the shape with rectangular subsections. Increasing the amount of ever smaller rectangles gives an infinitely more accurate approximation of the volume of the solid. It can be seen that a higher iteration of smaller rectangles gives a much more accurate approximation of the volume.
I have interests in fluid mechanics although my knowledge is for the most part fairly limited. Fluid Mechanics has many applications, one of which is basically aerodynamics for land vehicle design, and alot of multivariable differential calculus is used to determine fluid flow over surfaces by approximating surfaces and shapes as the sum of various functions in three dimensional space, like a 3-dimensional, multivariable riemman sum. Double and triple integrals can be performed by computer algorithms to determine ideal aerodynamic shape to optimize downforce in race cars, and fluid flow can be approximated by Partial differential equations, since fluid dynamics involves multivariable equations with partial derivatives. Multivariable calculus is very helpful in fluid dynamics since it involves vectors, and vector flow is used by Computational Fluid Dynamics software.
A venturi style ground effect in high performance cars can also optimize down force. The Venturi was also applied to Carbuerators, which used this partial vacuum concept to blend air and fuel for use in the combustion chambers, before EFI (Electronic Fuel Injection) and Direct Fuel Injection (direct injection into chamber) were fully implemented. Unfortunatley, venturis have a tendency to "ice up" on freezing cold days. Modern cars have become amazingly efficient with the implementation of electronic fuel injection, which allows a car to burn what a vintage carbuereted engine would fail to burn. This means that modern cars have surperior fuel economy and very clean emissions. A venturi style ground effect creates inverted lift in high performance cars can also optimize down force. Fluid Dynamics algorithms can be achieved through Stoke's Theorem, Divergence, and Greens Theorem as a basis among many more theorems. The venturi is integrated into the monocoque/unibody structure with air intakes which allows air to flow in, creating inverted lift in a partial vacuum of greater pressure over the venturi, pushing the car into the ground, allowing a higher speed when cornering, resulting in a higher G-turn force.
Automotive technology has, in the latest years, been advancing so fast that the FIA has had to put strict restrictions LMP and Formula 1 cars just so the car's performance isn't so extreme that drivers can still operate the car. These days, formula 1 engines run at exceptionally high Revs, typically maximizing near 20,000 rpm. This means that every second, the pistons in a Formula 1 car's engine makes about 334 revolutions before shifting up. This kind of RPM is pushing the engine's components to the limit, and the springs to control the movement of the intake and exhaust valves over the combustion chamber gets to a point where the up-down motion is so incredibly fast that severe valve float is a problem in Hyper performance vehicle design. The valves are vibrating with a resonant frequency that causes the valve float.
Beyond constant-acceleration Kinematic equations in physics, Ordinary Differential Equations can be used to derive velocity and position equations for real world movement including non-linear air resistance. This is why the Bugatti Veyron Super Sport needs a whole 200 hp more than the standard Veyron to achieve only a few mph faster top speed, because at those relative speeds the air resistance has grown exponentially relative to increase in velocity so much more power needs to be added to the car.
Thermodynamics and ideal gas laws are used in the design of internal combustion engines. Internal combustion engines in cars are considered open systems in thermodynamics, the engine has dependencies in changes from the surroundings outside the engine boundaries, including the intake of air and fuel through the intake valve, and after ignition from the spark plugs, exhaust exits, contrast to a isolated piston in an isolated cylinder, which would be considered a control mass closed system. Density is mathematically defined as the limit as volume approaches a volume differential, and as this volume differential approaches zero, density's inverse relationship (since Density= Lim (v to (dv/dt)) m/v), Density goes into infinity. As infinity is an irrational mathematical concept, to get around this you choose your volume differential to be the smallest possible value while retaining a definite rational density value. Pressure is the Limit as Area approaches Area differential of the expression Force Normal/ Area, so the same concept applies, but with area instead (Pressure= Lim (A to (dA/dt)) Fnormal/Area).
The average ideal stoichiometric ratio of air to gasoline in the combustion chamber of an architypical car is 14.7:1. Deviation from this typical standard in most cars results in a "lean burn" (excess air) or "rich burn" (excess fuel). Often, in mathematical thermodynamic analysis of automotive engines, Air-standard assumptions are made to simplify analysis since so much more air burns than relative fuel.
A hemi engine is developed as a hemi-spherical head of the combustion chamber is shaped by advanced 3-dimensional calculus.
In an internal combustion engine, one may lay out the camshafts in various ways in the design of the engine. A SOHC is a "single overhead cam system", and a DOHC is a "Dual-Overhead Cam system". When not an overhead system, pushrods are used to transmit the offset from the cam lobe to the rocker arm to open and close valves, reffered to as an OVH engine, or "Overhead Valves". The push rod is used since the camshaft is bellow the level of the valves atop the cylinder head.
Ordinary or Partial Differential Equations are used to shape camshafts and camshaft lobes. Timing belts are mathematically timed to relate the movement of the exhaust and intake valves with the crankshaft to move the pistons up and down. Many people question why timing belts are used in cars when engineers could use timing chains which don't risk blowing the engine since chains don't typically snap. The answer is that cars meant for very smooth and quiet operation such as luxury sedans should use a timing belt which is more appropriate for cars such as a Lexus or Mercedes Benz where as a Chain might be better suited for something like a Jeep Cherokee Classic or Toyota FJ Cruiser.
Differential Equations is critical for engineers in order to shape gear teeth and also ideal gear ratios. A rear differential's gear curvature is highly dependent on Differential equations for effective use. A cylinder or combustion chamber may have varying amounts of valves, both intake or exhaust. One can have 2 valves, one intake and one exhaust, or you can have 4, 2 exhaust and 2 intake for improved performance, and even 5 valves per cylinder. For optimal performance, most of the time you will find larger intake valves and smaller exhaust valves.
A major issue with Inline four cylinder engines are secondary force imbalances. Looking at a force summation, Sigma F in x and y components, the orientation of 4 pistons in a line creates a non-equilibrium in forces as the crankshaft rotates. Engineers solve this issue with engine balance shafts, and two are required to bring to engine to equilibrium for smooth operation. They feature counterweights on a shaft to balance engine forces.
One may increase the amount of air in the combustion chamber with a turbocharger, but this will involve a phenomenon known as "turbolag". Turbochargers use exhaust driven turbines for forced induction, cramming more air into the combustion chambers. There are also superchargers, which is also a forced induction system, compared to naturally aspirated engines. A turbo charger "whines" at a high pitch because it is running at about 200,000 to 300,000 RPM typically, on a car.
A catalytic converter consists of a honeycomb structure which uses chemical reactions to greatly reduce harmful pollutants and makes a car much less harmful to the environment. The catalyst consists of a ceramic monolith substrate which uses chemical reactions to convert highly harmful pollutants such as methane into water, oxygen, and carbon dioxide. Modern cars impact the environment about 1/100th that of a vintage car from the 1950s. In fact, a two-stroke lawnmower contributes about 50 times the affect of a modern car, and rickshaws in India contribute about 50 times as much, but The Colorado State University Engines and Energy Conversion Lab took care of that. Little performance may be lost but for most street cars, even performance and enthusiast oriented machines, the pros far outweigh the cons. Exhaust systems actually affect performance alot more than many people intuitively think.
Modern cars are filled with computer sensors for data aquisition of moving components and can quickly make adjustments many times every second to optimize performance. Modern cars feature an ECU or PCM, which is a small computer usually located near your glove compartment. If you drive any fairly modern car, your car is making millions of calculations every second to control your engine, and has Data Aquisition Systoms in which the oxygen sensor adjusts stoichiometric air:fuel ratio depending on the environment your car is driving in. This is all related to how the engine operates, all being meticulously controlled by a computer checking tables of data millions of times a second. Ignition and injection timing is optimized. Older modern cars have a distributor controlled by a computer, but very new cars have distributorless engines in which coils sit directly above the spark plugs, also controlled by the ECU.
Conservation of energy, conservation of momentum, force, and inertia is considered in crumple zone and crash safety design.
I own a 3rd generation Toyota Camry LE Sedan- Aluminum Alloy-head/iron block 2.2 Liter 16-valve 135 hp DOHC EFI In-line 4, 4 valves per cylinder, flat-faced cam follower with no rocker arms,soundproof body shell, steel monocoque unibody construction with asphalt composite sound insulation and adhesive bonding. Side Impact Door Beams, triple sealed doors, fluid filled engine mounts, dual engine balance shafts in the oil sump, Dolby Surround Sound, Direct Panel-to-Panel Bonding and one piece doors, Electronic Controlled Transmission, Overdrive, High Tensile Strength Steel unibody and shell, and shift lock override. The 3rd gen Camry or Camry Vienta/Scepter was one of the 1990s super touring series race cars. It competed in Austrailian Super Touring and South African Super Touring through FIA racing. Rod Millen took 2nd place in the Super Touring Camry in the 1997 North American Touring Car Championship. The car ran on a very highly tuned 2.0 Liter In line four making 300 horsepower... I believe it was naturally aspirated. This car is arguably one of the most highly engineered cars ever made, especially in just a standard midsize sedan. Its engineering and design is generally very highly regarded in the automotive industry, along with the 1989 Lexus LS400 and 1992 Lexus ES300, which the Camry was built from. Ford made a strong effort to keep Mary Walton's exposure of her book Car: A Drama of the American Workplace from becoming largely known outside of industry. Even the body styling is a marvel- To achieve the wide stance required, the engine bay and cradle had to be widened from the Japanese variant which was very difficult, and the stamping process was beyond what luxury marques were doing.
The tolerances and craftsmanship of the components in the car is another amazing story within itself. The engineering excellence of the 1992 Camry can be proven from calculus, in the definition of the Limit. 1992 Camry engineers designed every component so meticulously to have some of the tightest component tolerances in automotive history. The definition of a limit proves this by showing that if the ideal part dimensions are the Limit L, and the tolerance allowance is plus/minus Delta/Epsilon, then the 1992 Camry has among the smallest tolerance rectangles surrounding the Limit L, to symbolize each component individually. the precise definition of a limit gives the ideal limit itself, and the plus/minus epsilon/delta margin of error the L+/- delta on the x axis and L+/- Epsilon on the y axis forms a margin of error around the limit known as an "Error Tolerance Rectangle"... a 3 dimensional part is just the multivariable calculus version... The 1992 Camry's component tolerances have among the smallest of these tolerance rectangles in automotive history, which is quite expensive for mass production, but due to the yen dollar relationship when this car came out, Toyota could over-engineer every aspect, including the aerodynamically contoured body which was an incredibly rigid steel unibody monocoque with a thick, high tensile strength steel skin with extremely rigorous rust proofing. It is, in fact, one of the most well engineered cars ever created. The Lexus LS400 based styling of the body shell required an ultra-advanced state of the art stamping process at the time to form the compound curve of the Shoulder at the base of the C-pillars. Mercedes Benz and Audi weren't even capable of this in 1992. Additionally, it is one of the few cars featuring a one-piece roof lacking a rain gutter. BMW even reverse engineered the 1992 Toyota Camry sedan to understand, simply, how Toyota built such an incredible car and sell it in the midsize segment. Customers didn't know, but it was Toyota's secret way of "scaring" the competition of their technological capabilities. Toyota has cut down on this kind of engineering quality on each generation following the 3rd camry.
NVH in the automotive industry is Noise, Vibration, and Harshness Dampening, which involves computer data acquisition programs and computerized feedback loops.This was accomplished from advanced mathematics and physics including a topic in Ordinary Differential Equations, Laplace Transforms, which transforms variables in both ordinary and partial differential equations into a parameter through an exponential single integration, then the limit of said integration from zero to infinity transforming a differential equation into pure parameters, after a partial fraction decomposition, like a constant in a given state. Toyota assigned several hundred mechanical and electrical engineers on developing NVH, or Noise, Vibration Harshness, reduction. Computerized feedback control systems in the 1992 Camry including sophisticated engine management systems used the Laplace Transforms and performed it in a fraction of a second to reduce NVH and improve stability. Differential equations is also used for developing the state-of-the art non-synchronous automatic transmission of its day, specifically the gear teeth curvatures and I would assume fluid flow for the hydraulic fluid through the chambers. Toyota had developed an incredibly transmission in which gears feel like they simply glide seamlessly into place.
Laplace Transforms are also critical for making possible cruise control, and self driving technologies. Cruise Control is actually quite advanced. Your car needs tremendous DAQ (Data Aquisition) systems with feedback control loops that regulate engine rpm, and even senses a tend of gravitational acceleration or deceleration when driving downhill or uphill, respectively, in idle. This is because velocity is a directional vector in x-y coordinates, so if the car is traveling ideally perfectly straight, so it can be viewed from the side as a simple 2-D x-y dynamic coordinate, there is a gravitational weight MG pushing down, balanced by an equivalent force pushed up by the earth, known as your normal force. when the car ascends or descends, the car now has more of its velocity in the y direction, so the gravitational force acts in this direction, slowing the car as it drives uphill and speeding it up while going downhill. A cruise control system can logic through dynamics and physics and signal for braking pressure or a boost in engines rpm as appropriate.
Modern internal combustion engines require extensive use of Mathematics and physics for the design of the engine. The connecting rods have to be optimized as to when the piston will "Bottom out" upon its cycle. This is similar to a piston being heated until it hits stops in a closed system. The system is isobarric as the piston is free to move- if you neglect the frictional forces (which are cut down with engine lubricants as much as possible). Isobarric is a constant pressure state that is the result of a free moving piston that offsets the added heat to the system, coming from the ignition of the air fuel mix in the combustion chamber, in which a spark plug ignites the system. This heat forces the piston down to offset the pressure increase, and optimization is performed to see when and where to bottom out the con rods on the crankshaft. When a piston is forced to stop but heat is added, the system becomes isometric and non-isobaric. A fixed volume forces the piston to build up in pressure since the piston can't achieve boundary work (the single integral of the area under the PV curve at the vapor dome for working fluids), causing a vertical line up in the PV curve. The Camshafts, as stated before, are designed using differential equations. The connecting rods have to be designed using Engine Dynamics. The next question comes to be, how do you get this piston to return to its original location? Answer: you reject heat out of the system, so you open the exhaust valves and release the exhaust into the exhaust manifold. Thus, the piston is free to continue in its cycle. Your car probably accomplished all that in about 1/50th of a second of time. And it does it again. F1 cars can do this at over 300 times a second when almost red-lining the RPMs.
BDC and TDC refer to Bottom Dead Center and Top Dead Center, and compression ratio is a volume-dependent ratio, not a pressure ratio. The combustion chamber is at maximum volume at Bottom dead center and least volume at top dead center. Hot Rodders will sometimes play with the compression ratio by "shaving the heads" which makes TDC volume smaller. The piston bottoms out at bottom dead center. The Carnot efficiency of an engine is a maximum theoretical ideal efficiency of any given engine. The idea is to approach this efficiency as well as possible in reality, but it is physically impossible to achieve it no matter how advanced engine technology becomes because there will always be a hardware limitation of the engine that can NEVER reach the theoretical Carnot maximum efficiency. A perpetual motion machine isn't theoretically possible since it would be 100% efficient, and the carnot efficiency which is always under 100% can't even be achieved only approached. So, as engines advance, you could say that engines will approach carnot efficiency in the style of a Limit. Engineers can approach it, but the laws of physics prevent it from ever being achieved. Every heat engine and cycle is limited by a maximum Carnot efficiency.
EGR is knwon as Exhaust Gas Recirculation, which recirculates exhaust gases to lower combustion temperature and therefore reduces NOx emmisions (Nitrogen Oxide).
The ideal spark-ignition cycle is the Otto cycle, and the diesel cycle is seperate, with a lack of a spark plug, but with a glo plug to start off the engine
Engine knock can result from premature ignition in at least one cylinder in engines. This can cause pre-mature wear of the engine when it knocks.
Solid Mechanics is used to design automotive structures such as chassis and unibody monocoques. There is a requirement for a car's body structure to hold up during loads, and certain parts, known as crumple zones, must deform in a controlled manner in order to absorb energy and slow down the rate of deceleration. Strain gauges can measure this, and a 3-gage strain rossette is the only current method for measuring shear strain, since no other method is capable of experimentally measuring shear strain. Strain on a structure is a dimensionless measure of deformation per unit length of a deformable body, but expressed as a unit over the same unit, often denoted in epsilon or micro-epsilon. Thermal strain is a type of normal strain and therefore thermal strain can be set equal to normal strain to solve for a variable ((delta/Initial length)=(alpha*change in temperature)). In many cases, loaded systems can be solved using statics, and force and moment summations. However, in certain systems of standard and torsional loads, too many unknowns exist, and it becomes indeterminate. This now involves using Hooke's law, sigma=E(epsilon), which forms delta=FL/AE. For a temperature induced variation as well, it becomes delta=(FL/AE+(change in temp(coefficient of thermal expansion)(initial Length)). Now, the system is solvable. In torsional loading, angle of twist rho=TL/JG. J is the polar moment of inertia. When steel reaches what is known as the "yield point" in solid mechanics, it reaches a point where permenant deformation has occured.
The Lockheed Martin "Skunkworks" SR-71 Blackbird, debut in 1964, was a highly advanced jet capable of over Mach 3. To keep the fuselage from failing due to air friction, the jet was built out of a Carbon-Titanium composite body, and was currogated to allow massive expansion and contraction.
In materials science and engineering, atomic structure is critical in correctly selecting optimal materials for your engineering applications. Metallic bonding is a type of bonding in which the valence electrons form a "Sea of electrons", and this makes intuitive sense as to why metal alloys such as aluminum alloys or carbon steel is ductile. The electron sea allows large amounts of plastic deformation to occur. As an example, one reason aluminum is optimal for automotive shell structures is because not only is it light weight, making it ideal, but its ductility due to its metallically bonded atomic structure makes it ideal for energy absorbtion in car impacts. The valence electrons are not in fixed locations, and are non-directional in nature. Essentially, metalically bonded materials have de-localized bonds. Many polymers deform quite easily since the atomic makeup does a poor job resisting shear forces applied to the atomic structure, along the axis. Polymers are made up of primary covalent bonds which are linked by secondary bonds, known as Van Der Waals Bonds. Secondary bonding is vastly weaker than primary bonds. As a result, one can see that polymers require a low heat to dislocate the van der waals bonds. Modern Toyotas have had issues with melting dashboards since the polymer was engineered poorly as the secondary bonds were too weak for the environment the car will be subjected to. Bonding energy is directly proportional to melting temperature. This is intuitive and reasonable, since heat, or high temperature, is a measure of high energy. Then, it makes sense that a material with very strong bonds will require immense heats in order to melt the material, which requires the bonding in the solid state to break apart, or dislocate. Looking at an energy well, a steep curve with a large trough represents high bond energy, which will require a large energy to bring to the X axis, allowing for the dislocation of valence electrons, essentially melting the material. Elastic Modulus is dependent on interatomic bonding properties, not microstructure. Resultingly, treatment of metals and cold working will not change elastic modulus, which is the slope of the linear initial stress strain line. In fact, quantum mechanics even plays a role in materials engineering. The "Wave Particle Duality", which was discovered via the double-slit experiment, is a very strange phenomenon in which electrons may behave as particles or waves, and oddly, the act of observation may play a role in the outcome. According to a friend, the nuclear forces from the observational system influences the behavior of the electrons.
I'm not at the knowledge level of Engineering Explained's Jason Fenske, but he has helped me learn.
Here it is, almost nobody on facebook reads it LOL
Please, if anything is wrong, and some things are a bit assumed, let me know. I want to learn.
Rocket engine nozzles typically feature a shape that first converges then diverges. This is because the flow of the air fuel combustion reaction enters the nozzle at a subsonic velocity, below the speed of sound. As the nozzle converges, the flow's velocity increases to a sonic velocity that forms a shockwave infront of it as pressure decreases. It has reached a speed of sound with a Mach number of 1. Then the nozzle begins diverging, because the flow is supersonic. The conditions for supersonic flow are inverted, so the nozzle diverges to increase velocity. Pressure continues to decrease. In the design of the NASA space shuttle, the cooling system of the divergent supersonic flow rocket engines borrowed cooling techniques used in 1880s internal combustion engines.
Cars- what amazing marvels of technology. Perhaps one of the most taken for-granted products in people's lives. Cars are likley the most technologically complex possession in the average person's life. Modern cars are the result of exhaustive computational analysis in fluid mechanics to design an aerodynamic body, involving super computers calculating multivariable calculus and partial differential equations at incredible speed. The 1989 Lexus LS400 was the result of some 1400 engineers working tirelessly. Internal Combustion Engines are absurdly complex, involving fluid mechanics, thermodynamics, chemistry, and engine dynamics. Transmissions are even more mind boggling, containing approximatley 700 parts.
In designing automotive camshafts, when choosing calculus/differential equation based piecewise functions for your displacement model, one must choose a function which will not "run out" of derivatives from displacement in which ds/dt is velocity, in which dv/dt is acceleration, and da/dt becomes jerk. It is then often necessary to select a sinusoidal or cosine type function which derives and integrates between cosine and sine, and therefore does not encounter a "Dirac delta function", which results in infinity spikes starting at acceleration and passing on to jerk, which theoretically states that the cam lobe is experiencing zero stress and force. This is the opposite of the truth, as this would result in a sharply pointed cam lobe, which would experience massive stress concentration at its tip, which would rub off into a blunter normal shaped cam from the incredible stress. In calculus, these "Infinity spikes" are the results of vertical lines in the velocity diagram which creates discontinuities. A dwell is a location where a cam lobe has zero velocity and acceleration. Non-dwell piecewise functions at non-zero velocity and acceleration must be linked continuously to dwells with zero velocity and acceleration according to the fundamentals of cam design.
A multivariable Riemann sum in calculus can be used to approximate any 3 dimensional volume by approximating the shape with rectangular subsections. Increasing the amount of ever smaller rectangles gives an infinitely more accurate approximation of the volume of the solid. It can be seen that a higher iteration of smaller rectangles gives a much more accurate approximation of the volume.
I have interests in fluid mechanics although my knowledge is for the most part fairly limited. Fluid Mechanics has many applications, one of which is basically aerodynamics for land vehicle design, and alot of multivariable differential calculus is used to determine fluid flow over surfaces by approximating surfaces and shapes as the sum of various functions in three dimensional space, like a 3-dimensional, multivariable riemman sum. Double and triple integrals can be performed by computer algorithms to determine ideal aerodynamic shape to optimize downforce in race cars, and fluid flow can be approximated by Partial differential equations, since fluid dynamics involves multivariable equations with partial derivatives. Multivariable calculus is very helpful in fluid dynamics since it involves vectors, and vector flow is used by Computational Fluid Dynamics software.
A venturi style ground effect in high performance cars can also optimize down force. The Venturi was also applied to Carbuerators, which used this partial vacuum concept to blend air and fuel for use in the combustion chambers, before EFI (Electronic Fuel Injection) and Direct Fuel Injection (direct injection into chamber) were fully implemented. Unfortunatley, venturis have a tendency to "ice up" on freezing cold days. Modern cars have become amazingly efficient with the implementation of electronic fuel injection, which allows a car to burn what a vintage carbuereted engine would fail to burn. This means that modern cars have surperior fuel economy and very clean emissions. A venturi style ground effect creates inverted lift in high performance cars can also optimize down force. Fluid Dynamics algorithms can be achieved through Stoke's Theorem, Divergence, and Greens Theorem as a basis among many more theorems. The venturi is integrated into the monocoque/unibody structure with air intakes which allows air to flow in, creating inverted lift in a partial vacuum of greater pressure over the venturi, pushing the car into the ground, allowing a higher speed when cornering, resulting in a higher G-turn force.
Automotive technology has, in the latest years, been advancing so fast that the FIA has had to put strict restrictions LMP and Formula 1 cars just so the car's performance isn't so extreme that drivers can still operate the car. These days, formula 1 engines run at exceptionally high Revs, typically maximizing near 20,000 rpm. This means that every second, the pistons in a Formula 1 car's engine makes about 334 revolutions before shifting up. This kind of RPM is pushing the engine's components to the limit, and the springs to control the movement of the intake and exhaust valves over the combustion chamber gets to a point where the up-down motion is so incredibly fast that severe valve float is a problem in Hyper performance vehicle design. The valves are vibrating with a resonant frequency that causes the valve float.
Beyond constant-acceleration Kinematic equations in physics, Ordinary Differential Equations can be used to derive velocity and position equations for real world movement including non-linear air resistance. This is why the Bugatti Veyron Super Sport needs a whole 200 hp more than the standard Veyron to achieve only a few mph faster top speed, because at those relative speeds the air resistance has grown exponentially relative to increase in velocity so much more power needs to be added to the car.
Thermodynamics and ideal gas laws are used in the design of internal combustion engines. Internal combustion engines in cars are considered open systems in thermodynamics, the engine has dependencies in changes from the surroundings outside the engine boundaries, including the intake of air and fuel through the intake valve, and after ignition from the spark plugs, exhaust exits, contrast to a isolated piston in an isolated cylinder, which would be considered a control mass closed system. Density is mathematically defined as the limit as volume approaches a volume differential, and as this volume differential approaches zero, density's inverse relationship (since Density= Lim (v to (dv/dt)) m/v), Density goes into infinity. As infinity is an irrational mathematical concept, to get around this you choose your volume differential to be the smallest possible value while retaining a definite rational density value. Pressure is the Limit as Area approaches Area differential of the expression Force Normal/ Area, so the same concept applies, but with area instead (Pressure= Lim (A to (dA/dt)) Fnormal/Area).
The average ideal stoichiometric ratio of air to gasoline in the combustion chamber of an architypical car is 14.7:1. Deviation from this typical standard in most cars results in a "lean burn" (excess air) or "rich burn" (excess fuel). Often, in mathematical thermodynamic analysis of automotive engines, Air-standard assumptions are made to simplify analysis since so much more air burns than relative fuel.
A hemi engine is developed as a hemi-spherical head of the combustion chamber is shaped by advanced 3-dimensional calculus.
In an internal combustion engine, one may lay out the camshafts in various ways in the design of the engine. A SOHC is a "single overhead cam system", and a DOHC is a "Dual-Overhead Cam system". When not an overhead system, pushrods are used to transmit the offset from the cam lobe to the rocker arm to open and close valves, reffered to as an OVH engine, or "Overhead Valves". The push rod is used since the camshaft is bellow the level of the valves atop the cylinder head.
Ordinary or Partial Differential Equations are used to shape camshafts and camshaft lobes. Timing belts are mathematically timed to relate the movement of the exhaust and intake valves with the crankshaft to move the pistons up and down. Many people question why timing belts are used in cars when engineers could use timing chains which don't risk blowing the engine since chains don't typically snap. The answer is that cars meant for very smooth and quiet operation such as luxury sedans should use a timing belt which is more appropriate for cars such as a Lexus or Mercedes Benz where as a Chain might be better suited for something like a Jeep Cherokee Classic or Toyota FJ Cruiser.
Differential Equations is critical for engineers in order to shape gear teeth and also ideal gear ratios. A rear differential's gear curvature is highly dependent on Differential equations for effective use. A cylinder or combustion chamber may have varying amounts of valves, both intake or exhaust. One can have 2 valves, one intake and one exhaust, or you can have 4, 2 exhaust and 2 intake for improved performance, and even 5 valves per cylinder. For optimal performance, most of the time you will find larger intake valves and smaller exhaust valves.
A major issue with Inline four cylinder engines are secondary force imbalances. Looking at a force summation, Sigma F in x and y components, the orientation of 4 pistons in a line creates a non-equilibrium in forces as the crankshaft rotates. Engineers solve this issue with engine balance shafts, and two are required to bring to engine to equilibrium for smooth operation. They feature counterweights on a shaft to balance engine forces.
One may increase the amount of air in the combustion chamber with a turbocharger, but this will involve a phenomenon known as "turbolag". Turbochargers use exhaust driven turbines for forced induction, cramming more air into the combustion chambers. There are also superchargers, which is also a forced induction system, compared to naturally aspirated engines. A turbo charger "whines" at a high pitch because it is running at about 200,000 to 300,000 RPM typically, on a car.
A catalytic converter consists of a honeycomb structure which uses chemical reactions to greatly reduce harmful pollutants and makes a car much less harmful to the environment. The catalyst consists of a ceramic monolith substrate which uses chemical reactions to convert highly harmful pollutants such as methane into water, oxygen, and carbon dioxide. Modern cars impact the environment about 1/100th that of a vintage car from the 1950s. In fact, a two-stroke lawnmower contributes about 50 times the affect of a modern car, and rickshaws in India contribute about 50 times as much, but The Colorado State University Engines and Energy Conversion Lab took care of that. Little performance may be lost but for most street cars, even performance and enthusiast oriented machines, the pros far outweigh the cons. Exhaust systems actually affect performance alot more than many people intuitively think.
Modern cars are filled with computer sensors for data aquisition of moving components and can quickly make adjustments many times every second to optimize performance. Modern cars feature an ECU or PCM, which is a small computer usually located near your glove compartment. If you drive any fairly modern car, your car is making millions of calculations every second to control your engine, and has Data Aquisition Systoms in which the oxygen sensor adjusts stoichiometric air:fuel ratio depending on the environment your car is driving in. This is all related to how the engine operates, all being meticulously controlled by a computer checking tables of data millions of times a second. Ignition and injection timing is optimized. Older modern cars have a distributor controlled by a computer, but very new cars have distributorless engines in which coils sit directly above the spark plugs, also controlled by the ECU.
Conservation of energy, conservation of momentum, force, and inertia is considered in crumple zone and crash safety design.
I own a 3rd generation Toyota Camry LE Sedan- Aluminum Alloy-head/iron block 2.2 Liter 16-valve 135 hp DOHC EFI In-line 4, 4 valves per cylinder, flat-faced cam follower with no rocker arms,soundproof body shell, steel monocoque unibody construction with asphalt composite sound insulation and adhesive bonding. Side Impact Door Beams, triple sealed doors, fluid filled engine mounts, dual engine balance shafts in the oil sump, Dolby Surround Sound, Direct Panel-to-Panel Bonding and one piece doors, Electronic Controlled Transmission, Overdrive, High Tensile Strength Steel unibody and shell, and shift lock override. The 3rd gen Camry or Camry Vienta/Scepter was one of the 1990s super touring series race cars. It competed in Austrailian Super Touring and South African Super Touring through FIA racing. Rod Millen took 2nd place in the Super Touring Camry in the 1997 North American Touring Car Championship. The car ran on a very highly tuned 2.0 Liter In line four making 300 horsepower... I believe it was naturally aspirated. This car is arguably one of the most highly engineered cars ever made, especially in just a standard midsize sedan. Its engineering and design is generally very highly regarded in the automotive industry, along with the 1989 Lexus LS400 and 1992 Lexus ES300, which the Camry was built from. Ford made a strong effort to keep Mary Walton's exposure of her book Car: A Drama of the American Workplace from becoming largely known outside of industry. Even the body styling is a marvel- To achieve the wide stance required, the engine bay and cradle had to be widened from the Japanese variant which was very difficult, and the stamping process was beyond what luxury marques were doing.
The tolerances and craftsmanship of the components in the car is another amazing story within itself. The engineering excellence of the 1992 Camry can be proven from calculus, in the definition of the Limit. 1992 Camry engineers designed every component so meticulously to have some of the tightest component tolerances in automotive history. The definition of a limit proves this by showing that if the ideal part dimensions are the Limit L, and the tolerance allowance is plus/minus Delta/Epsilon, then the 1992 Camry has among the smallest tolerance rectangles surrounding the Limit L, to symbolize each component individually. the precise definition of a limit gives the ideal limit itself, and the plus/minus epsilon/delta margin of error the L+/- delta on the x axis and L+/- Epsilon on the y axis forms a margin of error around the limit known as an "Error Tolerance Rectangle"... a 3 dimensional part is just the multivariable calculus version... The 1992 Camry's component tolerances have among the smallest of these tolerance rectangles in automotive history, which is quite expensive for mass production, but due to the yen dollar relationship when this car came out, Toyota could over-engineer every aspect, including the aerodynamically contoured body which was an incredibly rigid steel unibody monocoque with a thick, high tensile strength steel skin with extremely rigorous rust proofing. It is, in fact, one of the most well engineered cars ever created. The Lexus LS400 based styling of the body shell required an ultra-advanced state of the art stamping process at the time to form the compound curve of the Shoulder at the base of the C-pillars. Mercedes Benz and Audi weren't even capable of this in 1992. Additionally, it is one of the few cars featuring a one-piece roof lacking a rain gutter. BMW even reverse engineered the 1992 Toyota Camry sedan to understand, simply, how Toyota built such an incredible car and sell it in the midsize segment. Customers didn't know, but it was Toyota's secret way of "scaring" the competition of their technological capabilities. Toyota has cut down on this kind of engineering quality on each generation following the 3rd camry.
NVH in the automotive industry is Noise, Vibration, and Harshness Dampening, which involves computer data acquisition programs and computerized feedback loops.This was accomplished from advanced mathematics and physics including a topic in Ordinary Differential Equations, Laplace Transforms, which transforms variables in both ordinary and partial differential equations into a parameter through an exponential single integration, then the limit of said integration from zero to infinity transforming a differential equation into pure parameters, after a partial fraction decomposition, like a constant in a given state. Toyota assigned several hundred mechanical and electrical engineers on developing NVH, or Noise, Vibration Harshness, reduction. Computerized feedback control systems in the 1992 Camry including sophisticated engine management systems used the Laplace Transforms and performed it in a fraction of a second to reduce NVH and improve stability. Differential equations is also used for developing the state-of-the art non-synchronous automatic transmission of its day, specifically the gear teeth curvatures and I would assume fluid flow for the hydraulic fluid through the chambers. Toyota had developed an incredibly transmission in which gears feel like they simply glide seamlessly into place.
Laplace Transforms are also critical for making possible cruise control, and self driving technologies. Cruise Control is actually quite advanced. Your car needs tremendous DAQ (Data Aquisition) systems with feedback control loops that regulate engine rpm, and even senses a tend of gravitational acceleration or deceleration when driving downhill or uphill, respectively, in idle. This is because velocity is a directional vector in x-y coordinates, so if the car is traveling ideally perfectly straight, so it can be viewed from the side as a simple 2-D x-y dynamic coordinate, there is a gravitational weight MG pushing down, balanced by an equivalent force pushed up by the earth, known as your normal force. when the car ascends or descends, the car now has more of its velocity in the y direction, so the gravitational force acts in this direction, slowing the car as it drives uphill and speeding it up while going downhill. A cruise control system can logic through dynamics and physics and signal for braking pressure or a boost in engines rpm as appropriate.
Modern internal combustion engines require extensive use of Mathematics and physics for the design of the engine. The connecting rods have to be optimized as to when the piston will "Bottom out" upon its cycle. This is similar to a piston being heated until it hits stops in a closed system. The system is isobarric as the piston is free to move- if you neglect the frictional forces (which are cut down with engine lubricants as much as possible). Isobarric is a constant pressure state that is the result of a free moving piston that offsets the added heat to the system, coming from the ignition of the air fuel mix in the combustion chamber, in which a spark plug ignites the system. This heat forces the piston down to offset the pressure increase, and optimization is performed to see when and where to bottom out the con rods on the crankshaft. When a piston is forced to stop but heat is added, the system becomes isometric and non-isobaric. A fixed volume forces the piston to build up in pressure since the piston can't achieve boundary work (the single integral of the area under the PV curve at the vapor dome for working fluids), causing a vertical line up in the PV curve. The Camshafts, as stated before, are designed using differential equations. The connecting rods have to be designed using Engine Dynamics. The next question comes to be, how do you get this piston to return to its original location? Answer: you reject heat out of the system, so you open the exhaust valves and release the exhaust into the exhaust manifold. Thus, the piston is free to continue in its cycle. Your car probably accomplished all that in about 1/50th of a second of time. And it does it again. F1 cars can do this at over 300 times a second when almost red-lining the RPMs.
BDC and TDC refer to Bottom Dead Center and Top Dead Center, and compression ratio is a volume-dependent ratio, not a pressure ratio. The combustion chamber is at maximum volume at Bottom dead center and least volume at top dead center. Hot Rodders will sometimes play with the compression ratio by "shaving the heads" which makes TDC volume smaller. The piston bottoms out at bottom dead center. The Carnot efficiency of an engine is a maximum theoretical ideal efficiency of any given engine. The idea is to approach this efficiency as well as possible in reality, but it is physically impossible to achieve it no matter how advanced engine technology becomes because there will always be a hardware limitation of the engine that can NEVER reach the theoretical Carnot maximum efficiency. A perpetual motion machine isn't theoretically possible since it would be 100% efficient, and the carnot efficiency which is always under 100% can't even be achieved only approached. So, as engines advance, you could say that engines will approach carnot efficiency in the style of a Limit. Engineers can approach it, but the laws of physics prevent it from ever being achieved. Every heat engine and cycle is limited by a maximum Carnot efficiency.
EGR is knwon as Exhaust Gas Recirculation, which recirculates exhaust gases to lower combustion temperature and therefore reduces NOx emmisions (Nitrogen Oxide).
The ideal spark-ignition cycle is the Otto cycle, and the diesel cycle is seperate, with a lack of a spark plug, but with a glo plug to start off the engine
Engine knock can result from premature ignition in at least one cylinder in engines. This can cause pre-mature wear of the engine when it knocks.
Solid Mechanics is used to design automotive structures such as chassis and unibody monocoques. There is a requirement for a car's body structure to hold up during loads, and certain parts, known as crumple zones, must deform in a controlled manner in order to absorb energy and slow down the rate of deceleration. Strain gauges can measure this, and a 3-gage strain rossette is the only current method for measuring shear strain, since no other method is capable of experimentally measuring shear strain. Strain on a structure is a dimensionless measure of deformation per unit length of a deformable body, but expressed as a unit over the same unit, often denoted in epsilon or micro-epsilon. Thermal strain is a type of normal strain and therefore thermal strain can be set equal to normal strain to solve for a variable ((delta/Initial length)=(alpha*change in temperature)). In many cases, loaded systems can be solved using statics, and force and moment summations. However, in certain systems of standard and torsional loads, too many unknowns exist, and it becomes indeterminate. This now involves using Hooke's law, sigma=E(epsilon), which forms delta=FL/AE. For a temperature induced variation as well, it becomes delta=(FL/AE+(change in temp(coefficient of thermal expansion)(initial Length)). Now, the system is solvable. In torsional loading, angle of twist rho=TL/JG. J is the polar moment of inertia. When steel reaches what is known as the "yield point" in solid mechanics, it reaches a point where permenant deformation has occured.
The Lockheed Martin "Skunkworks" SR-71 Blackbird, debut in 1964, was a highly advanced jet capable of over Mach 3. To keep the fuselage from failing due to air friction, the jet was built out of a Carbon-Titanium composite body, and was currogated to allow massive expansion and contraction.
In materials science and engineering, atomic structure is critical in correctly selecting optimal materials for your engineering applications. Metallic bonding is a type of bonding in which the valence electrons form a "Sea of electrons", and this makes intuitive sense as to why metal alloys such as aluminum alloys or carbon steel is ductile. The electron sea allows large amounts of plastic deformation to occur. As an example, one reason aluminum is optimal for automotive shell structures is because not only is it light weight, making it ideal, but its ductility due to its metallically bonded atomic structure makes it ideal for energy absorbtion in car impacts. The valence electrons are not in fixed locations, and are non-directional in nature. Essentially, metalically bonded materials have de-localized bonds. Many polymers deform quite easily since the atomic makeup does a poor job resisting shear forces applied to the atomic structure, along the axis. Polymers are made up of primary covalent bonds which are linked by secondary bonds, known as Van Der Waals Bonds. Secondary bonding is vastly weaker than primary bonds. As a result, one can see that polymers require a low heat to dislocate the van der waals bonds. Modern Toyotas have had issues with melting dashboards since the polymer was engineered poorly as the secondary bonds were too weak for the environment the car will be subjected to. Bonding energy is directly proportional to melting temperature. This is intuitive and reasonable, since heat, or high temperature, is a measure of high energy. Then, it makes sense that a material with very strong bonds will require immense heats in order to melt the material, which requires the bonding in the solid state to break apart, or dislocate. Looking at an energy well, a steep curve with a large trough represents high bond energy, which will require a large energy to bring to the X axis, allowing for the dislocation of valence electrons, essentially melting the material. Elastic Modulus is dependent on interatomic bonding properties, not microstructure. Resultingly, treatment of metals and cold working will not change elastic modulus, which is the slope of the linear initial stress strain line. In fact, quantum mechanics even plays a role in materials engineering. The "Wave Particle Duality", which was discovered via the double-slit experiment, is a very strange phenomenon in which electrons may behave as particles or waves, and oddly, the act of observation may play a role in the outcome. According to a friend, the nuclear forces from the observational system influences the behavior of the electrons.
#2
Nice paper...at least from my pint of view.  Your professor should give you a pretty decent grade on it. You obviously know more math, physics, and engineering than (probably) the majority of us here on CL, although we DO have some aeronautical, automotive, and other engineers here as CL members. I myself studied some of the things you did in high school and college, but not to the same extent....so I'm certainly not the one best-qualified to critique your paper.
Your professor should give you a pretty decent grade on it. You obviously know more math, physics, and engineering than (probably) the majority of us here on CL, although we DO have some aeronautical, automotive, and other engineers here as CL members. I myself studied some of the things you did in high school and college, but not to the same extent....so I'm certainly not the one best-qualified to critique your paper.
Nevertheless, at your own request, I will add a few comments about a couple of things you may (?) have overlooked....or chosen not to include.
First, In the paragraph you write about monocoque/unibody automotive frames, it can be noted that engineers have also obtained excellent results, particularly with smaller and compact cars, with the space-frame design and clip-on body panels. Although also used by the Smart-for-Two and a few others, the (probable) best example of this was with the hugely successful Saturn S-series cars of the 1990s. (in fact, although outside the scope of your paper, which doesn't deal with marketing, it can also be noted that Saturn's corporate problems started when they dropped the S-series line and replaced it with newer, more conventionally designed rebadges from other GM divisions).
Second, you mention the technique of shaving heads to increase compression-ratios. That works in the strictly compression department and more (theoretically) available power and efficiency, but can open up Pandora's box with other problems. All else equal, higher compression of the air-fuel in the cylinders means more engine heat, more physical stress on the internal parts from the engine's power-stroke, more likelihood of spark knock/detonation, and may require air/fuel-mixture enrichment or spark-timing retardation to compensate......which defeats the very purpose of a higher compression ratio in the first place. Of course, with computer-sensors monitioring each engine revolution and its firing conditions in the applicable cylinder, all these conditions can be finely adjusted each second to obtain best power and efficiency available without spark knock.
Third, the 3Gen Camry was indeed, for its size and price, superbly engineered from a durability/reliablity/NHV point.......no one can deny that...we've had more than one thread her on CL n that very subject. But, three decades before that, back in the 1960s, engineers at Ford and GM had already solved the NVH problem in spades, in their large, full-size upmarket cars (Cadillac, Lincoln, Buick Electra, Olds 98, Mercury Marquis, etc....) You are probably young, in your early-mid 20s, and have probably not had many chance to drive those cars. I remember them quite well. They were the very definition of rolling living-room cocoons, and driving one home from work after a hard day, when you were tired, was like lying in a Jacuzzi. This was possible because large Ford and GM cars back them used a body-on-frame design, soft coil springs, and higher-quality sound-asorbing materials inside. But, conversely, most of them, except maybe for the Pontiac Bonneville with the heavy-duty-suspension option, handled like boats. Chrysler vehicles, in contrast, had unibodies (except for the top-line Imperial) and the better-handling front torsion-bar/rear-leaf-spring setup, but that, along with more cheaply-done interiors, compromised the ride quality and noise-isolation some.
 Your professor should give you a pretty decent grade on it. You obviously know more math, physics, and engineering than (probably) the majority of us here on CL, although we DO have some aeronautical, automotive, and other engineers here as CL members. I myself studied some of the things you did in high school and college, but not to the same extent....so I'm certainly not the one best-qualified to critique your paper.
Your professor should give you a pretty decent grade on it. You obviously know more math, physics, and engineering than (probably) the majority of us here on CL, although we DO have some aeronautical, automotive, and other engineers here as CL members. I myself studied some of the things you did in high school and college, but not to the same extent....so I'm certainly not the one best-qualified to critique your paper. Nevertheless, at your own request, I will add a few comments about a couple of things you may (?) have overlooked....or chosen not to include.
First, In the paragraph you write about monocoque/unibody automotive frames, it can be noted that engineers have also obtained excellent results, particularly with smaller and compact cars, with the space-frame design and clip-on body panels. Although also used by the Smart-for-Two and a few others, the (probable) best example of this was with the hugely successful Saturn S-series cars of the 1990s. (in fact, although outside the scope of your paper, which doesn't deal with marketing, it can also be noted that Saturn's corporate problems started when they dropped the S-series line and replaced it with newer, more conventionally designed rebadges from other GM divisions).
Second, you mention the technique of shaving heads to increase compression-ratios. That works in the strictly compression department and more (theoretically) available power and efficiency, but can open up Pandora's box with other problems. All else equal, higher compression of the air-fuel in the cylinders means more engine heat, more physical stress on the internal parts from the engine's power-stroke, more likelihood of spark knock/detonation, and may require air/fuel-mixture enrichment or spark-timing retardation to compensate......which defeats the very purpose of a higher compression ratio in the first place. Of course, with computer-sensors monitioring each engine revolution and its firing conditions in the applicable cylinder, all these conditions can be finely adjusted each second to obtain best power and efficiency available without spark knock.
Third, the 3Gen Camry was indeed, for its size and price, superbly engineered from a durability/reliablity/NHV point.......no one can deny that...we've had more than one thread her on CL n that very subject. But, three decades before that, back in the 1960s, engineers at Ford and GM had already solved the NVH problem in spades, in their large, full-size upmarket cars (Cadillac, Lincoln, Buick Electra, Olds 98, Mercury Marquis, etc....) You are probably young, in your early-mid 20s, and have probably not had many chance to drive those cars. I remember them quite well. They were the very definition of rolling living-room cocoons, and driving one home from work after a hard day, when you were tired, was like lying in a Jacuzzi. This was possible because large Ford and GM cars back them used a body-on-frame design, soft coil springs, and higher-quality sound-asorbing materials inside. But, conversely, most of them, except maybe for the Pontiac Bonneville with the heavy-duty-suspension option, handled like boats. Chrysler vehicles, in contrast, had unibodies (except for the top-line Imperial) and the better-handling front torsion-bar/rear-leaf-spring setup, but that, along with more cheaply-done interiors, compromised the ride quality and noise-isolation some.
Last edited by mmarshall; 01-03-15 at 09:21 AM.
#3
I give you an A+ hehe 
The discussion here is really educational and informative. I do hope this thread stays alive and I do hope we can have more and more technical, analytical, quantitative, logical and empircal discussion here. Sure, I admit that personally, all of this is nosebleed stuff that highly complex.........but then again without this high technical knowledge, the cars that we know of today may not have existed.
Heck, I reckon that we may not have progressed past the Industrial Revolution without it.
So yup, in this case, the heroes are Mathematicians, Scientists and Engineers with their insanely-high level of knowledge, skill and expertise as well the amount of time and effort they put in that has allowed for the machines that we enjoy today
Anyways, I hope can contribute to this discussion as well (even if I'm not a mathematician or a scientist or an engineer)
To Gen3Camry and to other 'nerdy' peeps (sorry if I use the term here), I have some questions:
1) Bentley mentions that there Continental GT Speed car is able to suck in 4,000 liters of air that goes through its radiators. Wow that's a lot.
2) VW, Audi and Lexus mention the term 'moments of inertia' a lot in their press releases. What is it?
and
3) The RENESIS 13B-MSP Wankel Rotary Engine possesses a 'REULEAUX TRIANGLE' as it's centrepiece.
What makes such a shape so special and what factor does it play in the rotary engine?

Also, here's some copy-pasta info from Wolfram
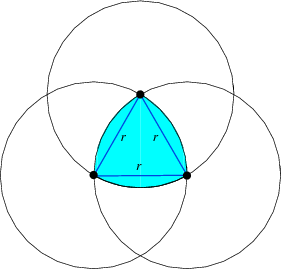
A curve of constant width constructed by drawing arcs from each polygon vertex of an equilateral triangle between the other two vertices. The Reuleaux triangle has the smallest area for a given width of any curve of constant width. Let the arc radius be r. Since the area of each meniscus-shaped portion of the Reuleaux triangle is a circular segment with opening angle theta=pi/3,
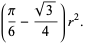
But the area of the central equilateral triangle with a=r is
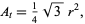
so the total area is then
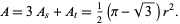
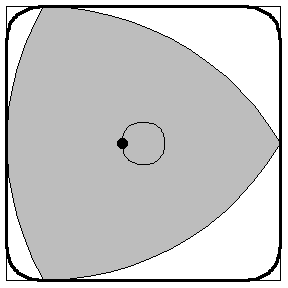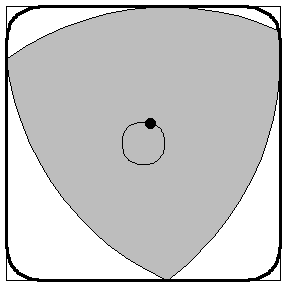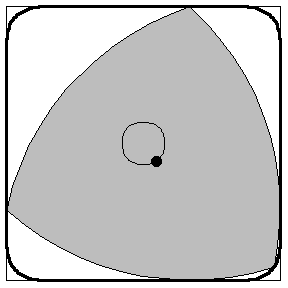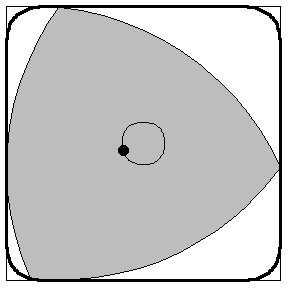
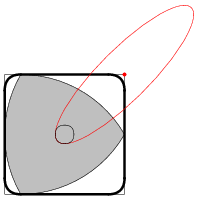
Because it can be rotated inside a square, as illustrated above, it is the basis for the Harry Watt square drill bit.

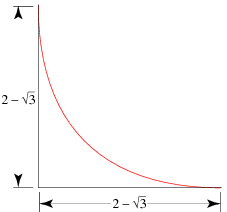
When rotated inside a square of side length 2 having corners at (+/-1,+/-1), the envelope of the Reuleaux triangle is a region of the square with rounded corners. At the corner (-1,-1), the envelope of the boundary is given by the segment of the ellipse with parametric equations
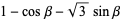
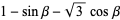
for beta in [pi/6,pi/3], extending a distance 2-sqrt(3) from the corner (Glei▀ner and Zeitler 2000). The ellipse has center (1,1), semimajor axis a=1+sqrt(3), semiminor axis b=sqrt(3)-1, and is rotated by 45 degrees, which has the Cartesian equation
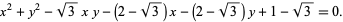
The fractional area covered as the Reuleaux triangle rotates is
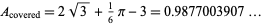
(OEIS A066666). Note that Glei▀ner and Zeitler (2000) fail to simplify their equivalent equation, and then proceed to assert that (8) is erroneous.

The geometric centroid does not stay fixed as the triangle is rotated, nor does it move along a circle. In fact, the path consists of a curve composed of four arcs of an ellipse (Wagon 1991). For a bounding square of side length 2, the ellipse in the lower-left quadrant has the parametric equations
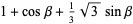
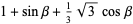
for beta in [pi/6,pi/3]. The ellipse has center (1,1), semimajor axis a=1+1/sqrt(3), semiminor axis b=1-1/sqrt(3), and is rotated by 45 degrees, which has the Cartesian equation
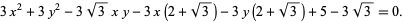
The area enclosed by the locus of the centroid is given by
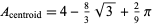
(Glei▀ner and Zeitler 2000; who again fail to simplify their expression). Note that the geometric centroid's path can be closely approximated by a superellipse
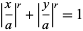
with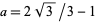
and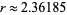
Source: http://mathworld.wolfram.com/ReuleauxTriangle.html
Whatever that means


The discussion here is really educational and informative. I do hope this thread stays alive and I do hope we can have more and more technical, analytical, quantitative, logical and empircal discussion here. Sure, I admit that personally, all of this is nosebleed stuff that highly complex.........but then again without this high technical knowledge, the cars that we know of today may not have existed.
Heck, I reckon that we may not have progressed past the Industrial Revolution without it.
So yup, in this case, the heroes are Mathematicians, Scientists and Engineers with their insanely-high level of knowledge, skill and expertise as well the amount of time and effort they put in that has allowed for the machines that we enjoy today

Anyways, I hope can contribute to this discussion as well (even if I'm not a mathematician or a scientist or an engineer)
To Gen3Camry and to other 'nerdy' peeps (sorry if I use the term here), I have some questions:
1) Bentley mentions that there Continental GT Speed car is able to suck in 4,000 liters of air that goes through its radiators. Wow that's a lot.
2) VW, Audi and Lexus mention the term 'moments of inertia' a lot in their press releases. What is it?
and
3) The RENESIS 13B-MSP Wankel Rotary Engine possesses a 'REULEAUX TRIANGLE' as it's centrepiece.
What makes such a shape so special and what factor does it play in the rotary engine?

Also, here's some copy-pasta info from Wolfram
Originally Posted by WOLFRAM MATHEMATICS WEBSITE

A curve of constant width constructed by drawing arcs from each polygon vertex of an equilateral triangle between the other two vertices. The Reuleaux triangle has the smallest area for a given width of any curve of constant width. Let the arc radius be r. Since the area of each meniscus-shaped portion of the Reuleaux triangle is a circular segment with opening angle theta=pi/3,
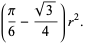
But the area of the central equilateral triangle with a=r is
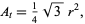
so the total area is then
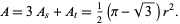

Because it can be rotated inside a square, as illustrated above, it is the basis for the Harry Watt square drill bit.


When rotated inside a square of side length 2 having corners at (+/-1,+/-1), the envelope of the Reuleaux triangle is a region of the square with rounded corners. At the corner (-1,-1), the envelope of the boundary is given by the segment of the ellipse with parametric equations
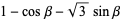
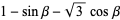
for beta in [pi/6,pi/3], extending a distance 2-sqrt(3) from the corner (Glei▀ner and Zeitler 2000). The ellipse has center (1,1), semimajor axis a=1+sqrt(3), semiminor axis b=sqrt(3)-1, and is rotated by 45 degrees, which has the Cartesian equation
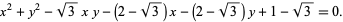
The fractional area covered as the Reuleaux triangle rotates is
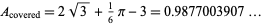
(OEIS A066666). Note that Glei▀ner and Zeitler (2000) fail to simplify their equivalent equation, and then proceed to assert that (8) is erroneous.


The geometric centroid does not stay fixed as the triangle is rotated, nor does it move along a circle. In fact, the path consists of a curve composed of four arcs of an ellipse (Wagon 1991). For a bounding square of side length 2, the ellipse in the lower-left quadrant has the parametric equations
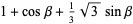
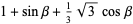
for beta in [pi/6,pi/3]. The ellipse has center (1,1), semimajor axis a=1+1/sqrt(3), semiminor axis b=1-1/sqrt(3), and is rotated by 45 degrees, which has the Cartesian equation
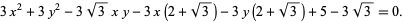
The area enclosed by the locus of the centroid is given by
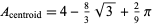
(Glei▀ner and Zeitler 2000; who again fail to simplify their expression). Note that the geometric centroid's path can be closely approximated by a superellipse
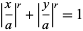
with
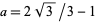
and
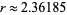
Source: http://mathworld.wolfram.com/ReuleauxTriangle.html


#4
Originally Posted by Blackraven
Whatever that means


 What I find most ingenious, though, about the Wankel Rotary engines is that the rotor, because it is offset, doesn't spin in a true circle or square, but actually spins around the central gear set inside a very slightly-pinched oval combustion chamber.....shaped more or less like a borderline figure-8. The lack of connection rods, up/down pistons, and traditional crankshaft allows high RPMs and smooth operation without balance-shafts and other anti-VH devices. Not being an engineer or engineering student like you though, though, that's about as much as I could describe it.
What I find most ingenious, though, about the Wankel Rotary engines is that the rotor, because it is offset, doesn't spin in a true circle or square, but actually spins around the central gear set inside a very slightly-pinched oval combustion chamber.....shaped more or less like a borderline figure-8. The lack of connection rods, up/down pistons, and traditional crankshaft allows high RPMs and smooth operation without balance-shafts and other anti-VH devices. Not being an engineer or engineering student like you though, though, that's about as much as I could describe it.
Last edited by mmarshall; 05-08-15 at 06:29 PM.
#5
Gen3Camry, that was awesome.
Very impressive how your education has taught you the theory very well and you have related it to real things to help give it more meaning. I'm sure that will help you whether you continue in ME or some other technical pursuit.
I didn't read all the way to the end and did not read it too critically, but I did not see anything needing correction. I used to teach Engineering at Stanford and would have loved to have a student like you in my class.
Good luck in whatever is next for you.
Very impressive how your education has taught you the theory very well and you have related it to real things to help give it more meaning. I'm sure that will help you whether you continue in ME or some other technical pursuit.
I didn't read all the way to the end and did not read it too critically, but I did not see anything needing correction. I used to teach Engineering at Stanford and would have loved to have a student like you in my class.
Good luck in whatever is next for you.
#6
The seemingly incoherent ramblings of an engineer. It is very difficult to put pen to paper and tell a story without knowing how it is going to end. I am happy you overcame that fear and conundrum and used the wide array of simple English words, engineering knowledge and jargons to stitch it all together.
Trending Topics
#12
That is so true. When we hire engineers fresh out of school, I have instituted a policy that for the six months they cannot work at a desk........ send them out in the field or to the manufacturing floor. This assignment forces them to learn rapidly to use their memory to process concepts & resulting reactions outside of a desktop or a laptop.
#13
That is so true. When we hire engineers fresh out of school, I have instituted a policy that for the six months they cannot work at a desk........ send them out in the field or to the manufacturing floor. This assignment forces them to learn rapidly to use their memory to process concepts & resulting reactions outside of a desktop or a laptop.
#15
I would think that especially in the mechanical engineering fields, that the new and upcoming engineers have zero practical experience. All they did as kids is play video games, they weren't out playing with go carts and building things. I feel this is why everything we have now is like it was designed by an idiot. I get a kick out of how the many things that were ironed out years ago with many thousands of old 50's or 40's dollars spent have either been forgotten or tossed out the door, or just never even known, an since the kids think they know everything they aren't going to ask an old person how to do it. I just wonder how many of these new engineers use the new nomenclature of the day, like "Breaks that stop the car" if they can't even get that correct how can they get anything else sorted out?



